Neuromorphic Unlimited Sampling

Unlimited sampling (US) is a computational sensing paradigm for high-dynamic range (HDR) acquisition of signals. The objective is to overcome the limitations in standard analog-to-digital converters (ADCs) where the dynamic range is fixed: signal that lies outside the fixed dynamic range saturates.

Unlimited sampling is an important problem in addressing signal representation in practical systems and has applications in almost all imaging systems. We propose a new technique for unlimited sampling using a neuromorphic encoder. Our system is power efficient, simple to implement in practice, and most importantly, does not require oversampling.

Computational Modulo Sampling

Computational modulo sampling is a framework for unlimted sampling that uses a self-reset ADC (SR-ADC) as opposed to a standard ADC, where a continuous-time signal \(f(t)\) is first folded using the continuous-domain modulo operator before acquisition. The idea of computational unlimited sampling was first proposed by Dr Ayush Bhandari, currently at Imperial College London. The continuous-time modulo operator with parameter \(\lambda\) is defined as

\[f\mapsto \mathcal{M}_{\lambda}\{f\} = 2\lambda\left[\frac{f}{2\lambda}+\frac{1}{2}\right]-\lambda,\]

where \([\cdot]\) defines the fractional part of the argument. The modulo operator restricts the dynamic range to the interval \([-\lambda,+\lambda]\) and enables acquisition of high-dynamic range (in principle, unlimited) acquisition.

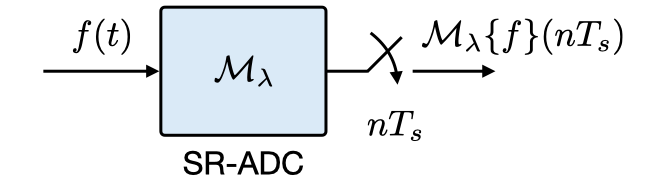
Fig. 1: What happens in a computational unlimited sampling setup.

Reconstruction of the high-dynamic range signal from samples of \(\mathcal{M}_{\lambda}\{f\}\) requires oversampling as compared to the Nyquist rate of \(f\). Further, for practical deployment of unlimited sampling, specialised hardware is required. This can indeed be a practical bottleneck! Oversampling is expensive, and adds to the cost of replacing the existing standard ADC with a self-reset ADC. Our solution addresses this problem and is as simple as using a nonlinear filter before acquisition!

The Neuromorphic Unlimited Sampling Framework

At the heart of our solution is the neuromorphic encoder, which is a bio-inspired acquisition device that has been successfully deployed in making efficient video acquisition systems. For more on neuromorphic video acquisition, check out the work from the Robotics and Perception Group.

Neuromorphic encoders are opportunistic devices that record signals as a stream of events that denote a change in the input by a constant. The signal is represented as a sequence of 2-tuples, each constituting the time instant and the polarity of change.

Fig. 2: Schematic of a neuromorphic encoder. The output is a sequence of 2-tuples characterising the time instant and polarity of change in the absolute-value of the signal by the dynamic-range of the ADC (Kamath & Seelamantula, 2023).

Neuromorphic encoders are of practical interest as they do not record any measurements when there is no significant change in the signal. The key observation for unlimited sampling is that the difference signal \(v(t)\) is a folded version of the input signal \(f(t)\), and is completely accommodated in the range \([-\lambda, +\lambda]\). In essence, the signal \(v(t)\) is a polarity dependent modulo operator acting on the input signal as

\[f\mapsto v = \mathcal{F}_\lambda\{f\}.\]

The in-built folding in the neuromorphic encoder along with its opportunistic nature makes it a perfect fit for unlimited sampling.

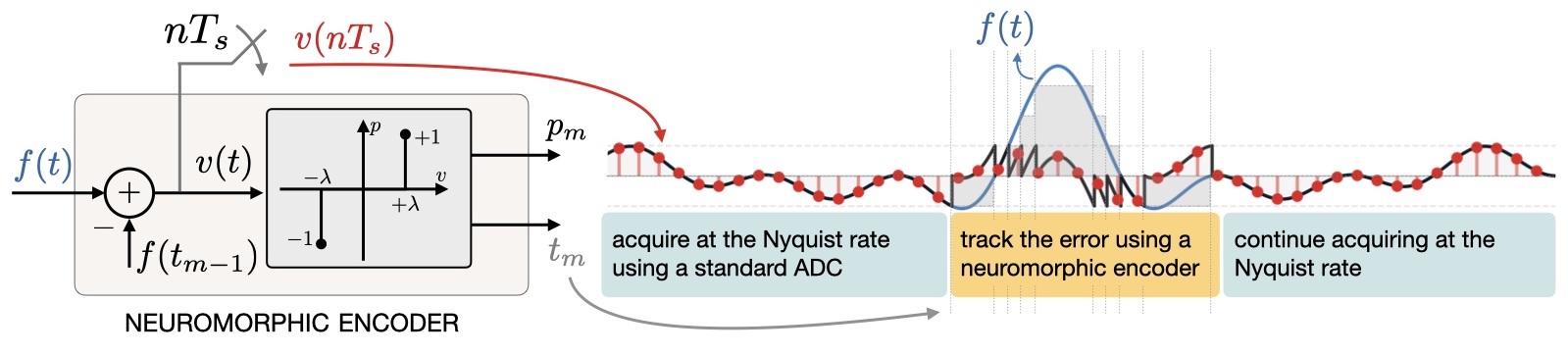
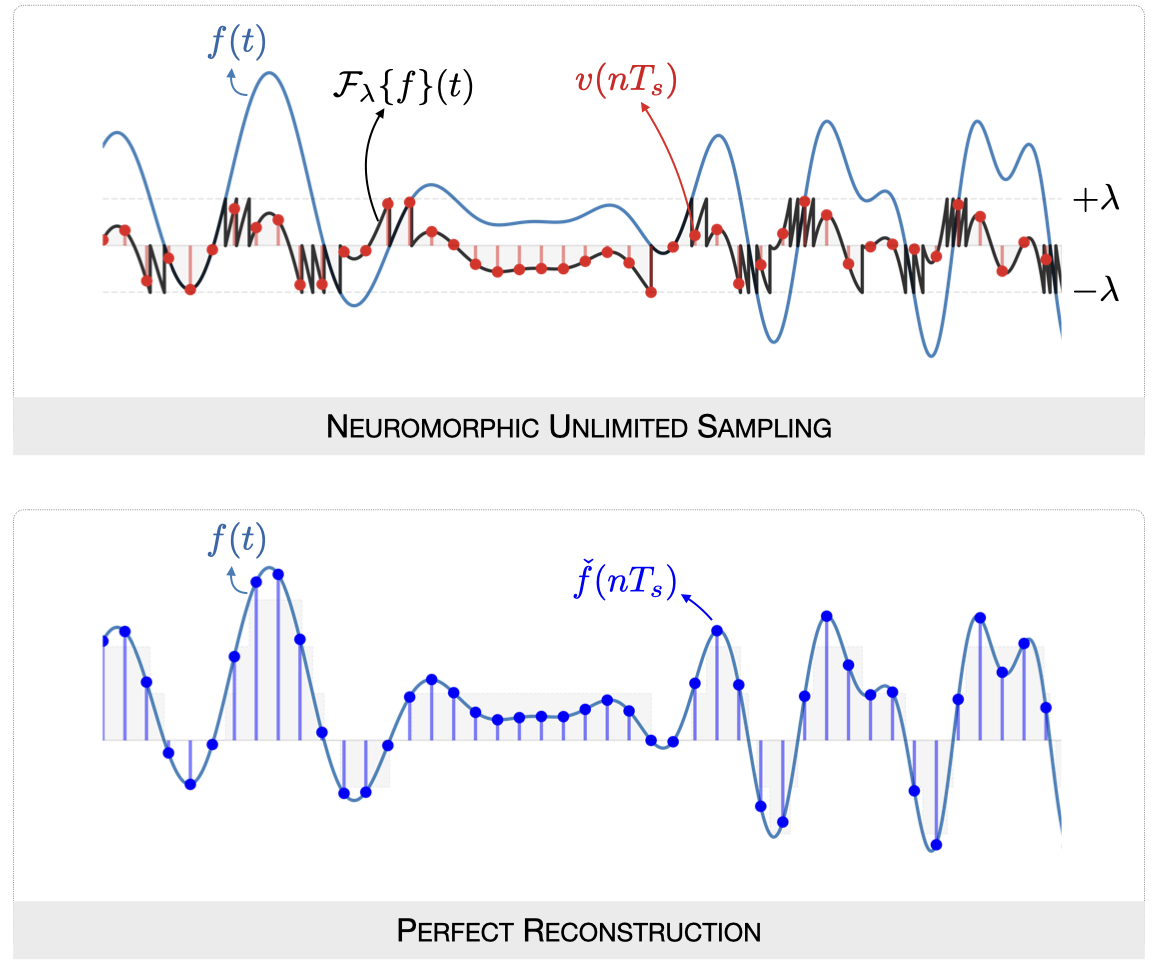
Fig. 3: Unlimited sampling using a neuromorphic encoder: The accompanying ADC operates at the Nyquist rate and at full precision. The error incurred due to folding is tracked using the neuromorphic encoder allowing real-time reconstruction.

Similar to modulo sampling, the error signal \(f(t)-v(t)\) is a piecewise constant signal with amplitude quantised to multiples of \(\lambda\). In computational modulo sampling, the error signal is estimated from oversampled measurements of the folded signal using the repeated finite-difference algorithm. In neuromorphic unlimited sampling, the error signal is captured succinctly using the output of the neuromorphic encoder as

\[\eta_f(t) = \sum_m \lambda\mathcal{S}\{p_m\} 1_{[t_m,t_{m+1}]}(t),\]

where \(\mathcal{S}\) denotes the cumulative summation operator. Therefore, no oversampling is required! Uniform samples of the folded signal \(v\) captures the high-dynamic-range information in the input signal, achieving unlimited sampling!

Additional measurements are made using the neuromorphic encoder opportunistically, i.e., only when the signal goes beyond the dynamic range while consuming much less power than the ADC. We also show that the maximal rate of additional measurements that may be obtained decays with the dynamic range. Our perfect reconstruction strategy only requires addition of a residual signal constructed using the compressed representation of the error signal, which can be achieved in real time.

Fig. 4: Demonstration of neuromorphic sampling and perfect reconstruction.

Our patented unlimited sampling hardware using simple and cost-effective components in-house (Kulur et al., 2024). The neuromorphic unlimited sampling scheme is such that the neuromorphic encoder can be plugged into an existing acquisition system to achieve unlimited sampling, akin to a prefilter typically used in sampling, and does not require specialised hardware such as the self-reset ADC. In hardware, we demonstrate HDR acquisition and real-time reconstruction of synthetic signals. We show that neuromorphic unlimited sampling operates at the Nyquist rate of the signal, while opportunistically recording compressed measurements. Our demonstration was presented at the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2024, in Seoul Korea 2024, in the Show-and-tell Demos (Kulur et al., 2024). A detailed theoretical exposition is available in our paper (Kamath & Seelamantula, 2024) which was also presented at IEEE ICASSP 2024. The extension of this theory to a larger class of signals including video signals is going to be presented at the IEEE ICASSP 2025 (Kamath & Seelamantula, 2025).

The hardware contributions to this project are in collaboration with Shreyas, Shreyansh, Satyapreet and Dr Thakur at NeuRonICS, Department of Electronic Systems Engineering, IISc. Bengaluru.

Computational Modulo Sampling

The Neuromorphic Unlimited Sampling Framework

References

2025

2024

2023